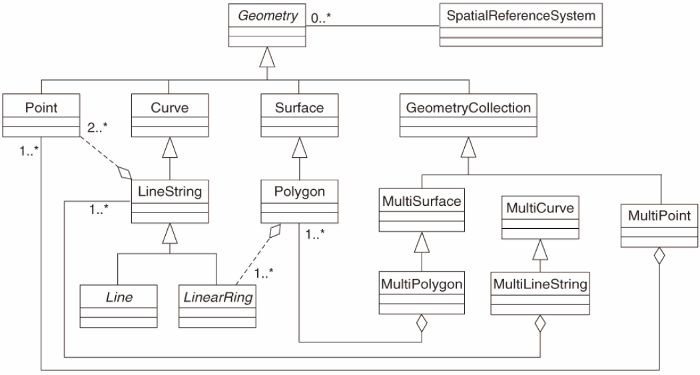
Simple Feature Model¶
Note
| Fecha | Autores |
|---|---|
| 1 Noviembre 2012 |
|
| 15 Octubre 2013 |
|
©2012 Micho García
Excepto donde quede reflejado de otra manera, la presente documentación se halla bajo licencia : Creative Commons (Creative Commons - Attribution - Share Alike: http://creativecommons.org/licenses/by-sa/3.0/deed.es)
OGC y el Simple Feature Model¶
La OGC o Open Geospatial Consortium, define unas normas que serán utilizadas para la definición posterior de las geometrías. Estas son la SFA y la SQL/MM. Según esta última, las geometrías se definirán en función del siguiente esquema de herencia:
Dentro de este esquema se definen tres tipos diferentes de geometrías:
- Geometrías abstractas, que sirven para modelar el comportamiento de las geometrías que heredan de ellas.
- Geometrías básicas, son las principales de PostGIS, soportadas desde los inicios de este y que soportan un análisis espacial completo.
- Geometrías circulares, geometrías que soportan tramos circulares
Dimensión de una geometría¶
El concepto de dimensión se explica de una manera sencilla mediante el uso de algunos ejemplos:
- una entidad de tipo punto, tendrá dimensión 0
- una de tipo linea, tendrá dimensión 1
- una de tipo superficie, tendrá una dimensión igual a 2.
En PostGIS utilizando una función especial podremos obtener el valor de esta dimensión. Si se trata de una colección de geometrías, el valor que se obtendrá será el de la dimensión de mayor valor de la colección.
Interior, contorno y exterior de las geometrías¶
Las definiciones las encontraremos en la norma. A continuación se indican los valores para las geometrías básicas.
Tipos de geometría Interior Contorno ST_Point El propio punto o puntos Vacio ST_Linestring Puntos que permanecen cuando contorno se elimina Dos puntos finales ST_MultiLinestring Idem Puntos de contorno de un nº impar de elementos ST_Polygon Puntos del interior de los anillos Conjunto de anillos exterior e interior (Rings) ST_Multipolygon Idem Conjunto de anillos exterior e interior (Rings)
WKT y WKB¶
WKT es el acrónimo en inglés de Well Known Text, que se puede definir como una codificación o sintaxis diseñada específicamente para describir objetos espaciales expresados de forma vectorial. Los objetos que es capaz de describir son: puntos, multipuntos, líneas, multilíneas, polígonos, multipolígonos, colecciones de geometría y puntos en 3 y 4 dimensiones. Su especificación ha sido promovida por un organismo internacional, el Open Geospatial Consortium, siendo su sintaxis muy fácil de utilizar, de forma que es muy generalizado su uso en la industria geoinformática. De hecho, WKT es la base de otros formatos más conocidos como el KML utilizado en Google Maps y Google Earth.
Muchas de las bases de datos espaciales, y en especial Postgresql, utiliza esta codificación cuando se carga la extensión PostGIS. Existe una variante de este lenguaje, pero expresada de forma binaria, denominada WKB (Well Know Binary), también utilizada por estos gestores espaciales, pero con la ventaja de que al ser compilada en forma binaria la velocidad de proceso es muy elevada.
A efectos prácticos la sintaxis WKT consta de una descripción de los vértices que componen la geometría. Para que esta forma de especificar las geometrías tengan sentido deben de acompañarse de una indicación de la referencia espacial o proyección cartográfica utilizada en dicho vector.
Ejemplos de sintaxis:
Punto: POINT(30 50)
Línea: LINESTRING(1 1, 5 5, 10 10, 20 20)
Multilínea: LINESTRING( (1 1, 5 5, 10 10, 20 20),(20 30, 10 15, 40 5) )
Polígono simple: POLYGON ((0 0, 10 0, 10 10, 0 0))
Varios polígono en una sola geometría (multipolígono): POLYGON ( (0 0, 10 0, 10 10, 0 10, 0 0),( 20 20, 20 40, 40 40, 40 20, 20 20) )
Geometrías de distinto tipo en un sólo elemento: GEOMETRYCOLLECTION(POINT(4 6),LINESTRING(4 6,7 10))
Punto vacío: POINT EMPTY
Multipolígono vacío: MULTIPOLYGON EMPTY
WKB acrónimo de Well Known Binary es la variante de este lenguaje, pero expresada de forma binaria, también utilizada por los gestores espaciales, pero con la ventaja de que al ser compilada en forma binaria la velocidad de proceso es muy elevada.
Tipos de datos espaciales¶
Una base de datos ordinaria tiene cadenas, fechas y números. Una base de datos añade tipos adicionales para georreferenciar los objetos almacenados. Estos tipos espaciales abstraen y encapsulan estructuras tales como el contorno y la dimensión.
De forma simplificada, tenemos los siguientes tipos de datos espaciales:
Tipo de geometria WKT POINT “POINT(0 0)” LINESTRING “LINESTRING(0 0, 1 1, 2 2, 3 4)” POLYGON “POLYGON(0 0, 0 1, 1 1, 0 0)” MULTIPOINT “MULTIPOINT(0 0, 1 1, 2 2)” MULTILINESTRING “MULTILINESTRING ((10 10, 2 2, 10 40), (40 40, 30 30, 40 20, 30 10))” MULTIPOLYGON “MULTIPOLYGON (((3 2, 0 0, 5 4, 3 2))” GEOMETRY COLLECTION
- “GEOMETRYCOLLECTION(
- POINT(4 6),LINESTRING(4 6,7 10))”
Definición de geometrías básicas¶
Point y Multipoint¶
- Geometrias con 0 dimensiones
- El contorno es el conjunto vacio
- Una geometría Multipoint es simple si no tiene ningún punto repetido
Linestring¶
- Geometrias de 1 dimensión
- Simple si no pasa por el mismo punto dos veces
- Cerrada si su punto inicial y final es el mismo
- El contorno si es cerrada es el conjunto vacio
- El contorno si no es cerrada son su punto final e inicial
- Si es simple y cerrada es un anillo (Ring)
Multilinestring¶
- Geometrías de 1 dimensión
- Cerrada si todos sus elementos son cerrados
- Si es cerrada su contorno es el conjunto vacio
Polygon¶
- Geometrías de 2 dimensiones
- Contiene un único interior conectado
- Tiene un anillo exterior y 0 o más anillos interiores
- El contorno es un conjunto de lineas cerradas que se corresponden con sus contornos exterior e interior
Multipolygon¶
- El interior de cualquiera de las superficies que contiene no puede intersecar
- El contorno de cualquiera de las superficies que contiene puede intersecar pero solo en un número finito de puntos
- Son simples
Referencias¶
Well Known Text en Wikipedia http://en.wikipedia.org/wiki/Well-known_text
Lesson 2. Simple Feature Model [EN] http://manual.linfiniti.com/en/postgis/simple_feature_model.html
Simple Feature Acces in Wikipedia [EN] http://en.wikipedia.org/wiki/Simple_Feature_Access