Análisis espacial¶
Note
| Fecha | Autores |
|---|---|
| 1 Noviembre 2012 |
|
| 15 Octubre 2013 |
|
©2012 Micho García
Excepto donde quede reflejado de otra manera, la presente documentación se halla bajo licencia : Creative Commons (Creative Commons - Attribution - Share Alike: http://creativecommons.org/licenses/by-sa/3.0/deed.es)
El análisis de datos con SIG tiene por finalidad descubrir estructuras espaciales, asociaciones y relaciones entre los datos, así como modelar fenómenos geográficos. Los resultados reflejan la naturaleza y calidad de los datos, además de la pertinencia de los métodos y funciones aplicadas. Las tareas y transformaciones que se llevan a cabo en el análisis espacial precisan datos estructurados, programas con las funciones apropiadas y conocimientos sobre la naturaleza del problema, para definir los métodos de análisis.
El proceso convierte los datos en información útil para conocer un problema determinado. Es evidente que los resultados del análisis espacial añaden valor económico y, sobre todo, información y conocimiento a los datos geográficos
Operadores espaciales¶
Estos son los encargados de realizar operaciones geométricas entre las geometrías que se les pasa como argumentos. Están definidos en la norma SFA y PostGIS soporta todos ellos.
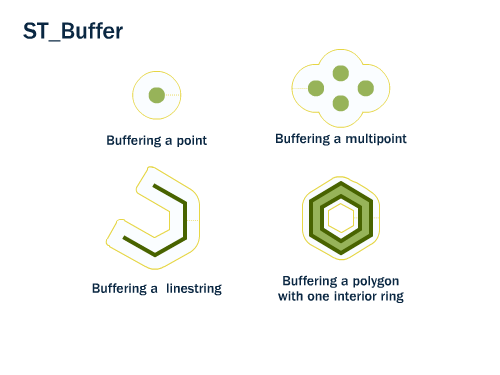
Buffer¶
Es el conjunto de puntos situados a una determinada distancia de la geometría
Acepta distancias negativas, pero estas en lineas y puntos devolverán el conjunto vacio.
Práctica¶
El uso de las funciones espaciales de PostGIS en unión con las funciones de agregación de PostgreSQL nos da la posibilidad de realizar análisis espaciales de datos agregados. Una característica muy potente y con diversas utilidades. Como ejemplo, vamos a ver la estimación proporcional de datos censales, usando como criterio la distancia entre elementos espaciales.
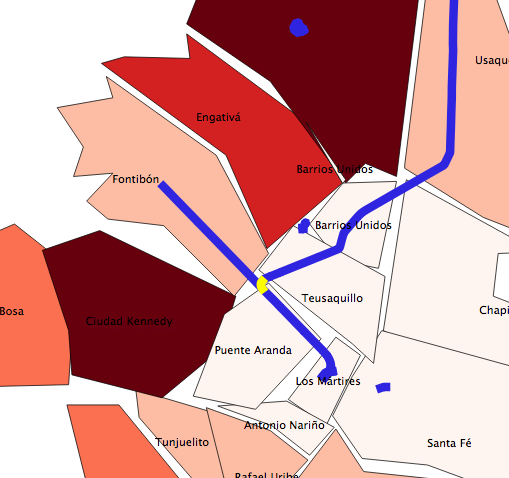
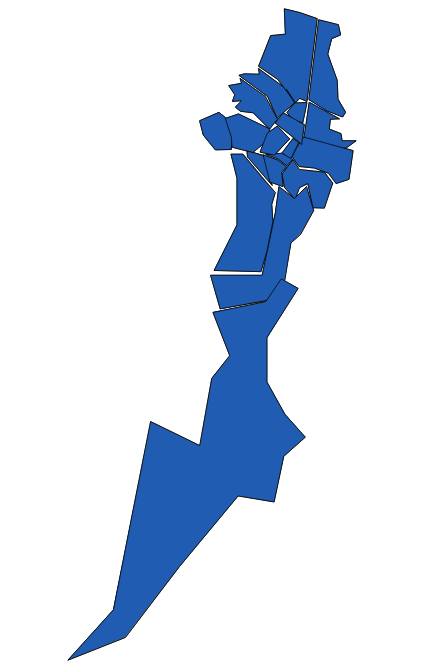
Tomemos como base los datos vectoriales de los barrios de Bogotá y los datos vectoriales de vías de ferrocarril (tablas barrios_de_bogota y railways, respectivamente). Fijémonos en una línea de ferrocarril que cruza 3 barrios (Fontibón, Puente Aranda, Los Mártires)
En la imagen, se han coloreado los polígonos de los barrios, de manera que los colores más claros suponen menos población.
Construyamos ahora un buffer de 1km alrededor de dicha línea de ferrocarril. Es de esperar que las personas que usen la línea sean las que vivan a una distancia razonable. Para ello, creamos una nueva tabla con el buffer:
#CREATE TABLE railway_buffer as
SELECT
1 as gid,
ST_Transform(ST_Buffer(
(SELECT ST_Transform(geom, 21818) FROM railways WHERE gid = 2), 1000, 'endcap=round join=round'), 4326) as geom;
Hemos usado la función ST_Transform para pasar los datos a un sistema de coordenadas proyectadas que use el metro como unidad de medida, y así poder especificar 1000m. Otra forma habría sido calcular cuántos grados suponen un metro en esa longitud, y usar ese número como parámetro para crear el buffer (más información en http://en.wikipedia.org/wiki/Decimal_degrees).
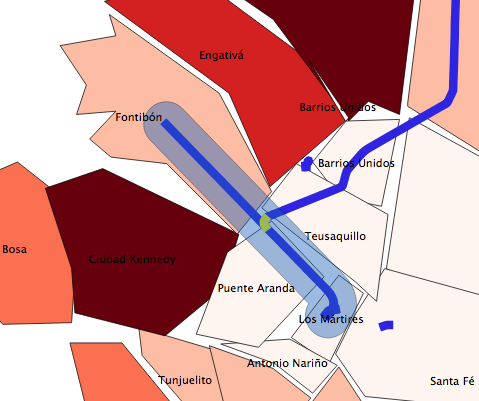
Al superponer dicho buffer sobre la línea, el resultado es éste:
Como se observa, hay 4 barrios que intersectan con ese buffer. Los tres anteriormente mencionados y Teusaquillo.
Una primera aproximación para saber la población potencial que usará el ferrocarril sería simplemente sumar las poblaciones de los barrios que el buffer intersecta. Para ello, usamos la siguiente consulta espacial:
# SELECT SUM(b.population) as pop
FROM barrios_de_bogota b JOIN railway_buffer r
ON ST_Intersects(b.geom, r.geom)
Esta primera aproximación nos da un resultado de 819892 personas.
No obstante, mirando la forma de los barrios, podemos apreciar que estamos sobre-estimando la población, si utilizamos la de cada barrio completo. De igual forma, si contáramos solo los barrios cuyos centroides intersectan el buffer, probablemente infraestimaríamos el resultado.
En lugar de esto, podemos asumir que la población estará distribuida de manera más o menos homogénea (esto no deja de ser una aproximación, pero más precisa que lo que tenemos hasta ahora). De manera que, si el 50% del polígono que representa a un barrio está dentro del área de influencia (1 km alrededor de la vía), podemos aceptar que el 50% de la población de ese barrio serán potenciales usuarios del ferrocarril. Sumando estas cantidades para todos los barrios involucrados, obtendremos una estimación algo más precisa. Habremos realizado una suma proporcional.
Para realizar esta operación, vamos a construir una función en PL/pgSQL. Esta función la podremos llamar en una query, igual que cualquier función espacial de PostGIS:
#CREATE OR REPLACE FUNCTION public.proportional_sum(geometry, geometry, numeric)
RETURNS numeric AS
$BODY$
SELECT $3 * areacalc FROM
(
SELECT (ST_Area(ST_Intersection($1, $2))/ST_Area($2))::numeric AS areacalc
) AS areac;
$BODY$
LANGUAGE sql VOLATILE
Esta función toma como argumentos las dos geometrías a intersectar y el valor total de población del cuál queremos estimar la población proporcional que usará el tren. Devuelve el número con la estimación. La operación que hace es simplemente multiplicar la proporción en la que los barrios se solapan con la zona de interés por la cantidad a proporcionar (la población).
La llamada a la función es como sigue:
# SELECT ROUND(SUM(proportional_sum(a.geom, b.geom, b.population))) FROM
railway_buffer AS a, barrios_de_bogota as b
WHERE ST_Intersects(a.geom, b.geom)
GROUP BY a.gid;
En este caso, el resultado obtenido es 248217, que parece más razonable.
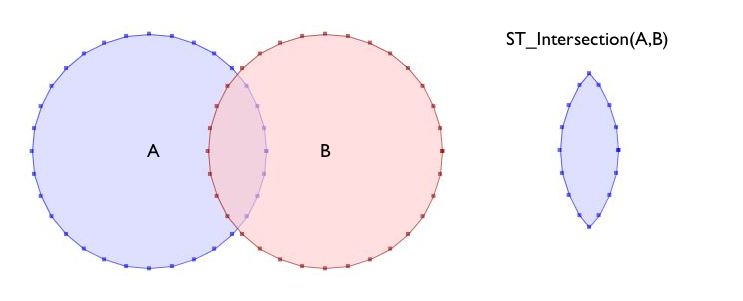
Intersección¶
Genera una geometría a partir de la intersección de las geometrías que se les pasa como parámetros.
¿Cúal es el area en común de dos círculos situados en los puntos (0 0) y (3 0) de radio 2?:
SELECT ST_AsText(ST_Intersection(
ST_Buffer('POINT(0 0)', 2),
ST_Buffer('POINT(3 0)', 2)
));
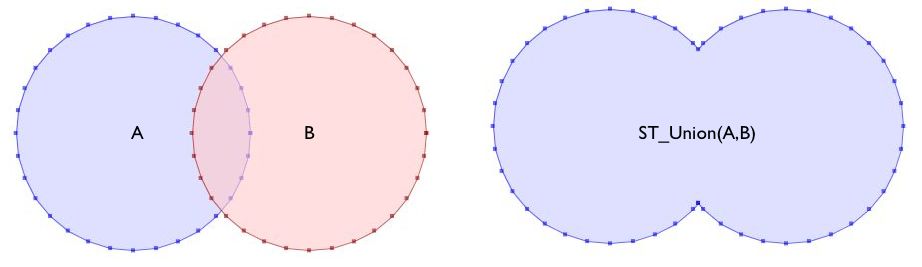
Unión¶
Al contrario que en el caso anterior, la unión produce un una geometría común con las geometrías que se le pasa a la función como argumento. Esta función acepta como parámetro dos opciones, las geometrías que serán unidas:
ST_Union(Geometría A, Geometría B)
o una colección de geometrías:
ST_Union([Geometry])
Práctica¶
Una primera aproximación podría ser usar la versión agregada de ST_Union, que toma como entrada un conjunto de geometrías y devuelve la unión de las mismas también como geometría. El conjunto de geometrías lo obtenemos gracias al uso de GROUP BY, que agrupa las filas por un campo común (en este caso, el campo city, que en todos los casos tiene el valor Bogota).
Usamos adicionalmente la función ST_SnapToGrid para ajustar la geometría de salida lo más posible a la rejilla regular definida por su origen y su tamaño de celda.
La consulta SQL es ésta:
#CREATE TABLE bogota AS
SELECT ST_Union(ST_SnapToGrid(geom,0.0001))
FROM barrios_de_bogota
GROUP BY city;
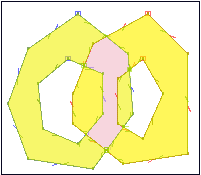
Y el resultado es el conjunto de polígonos, algo más suavizados:
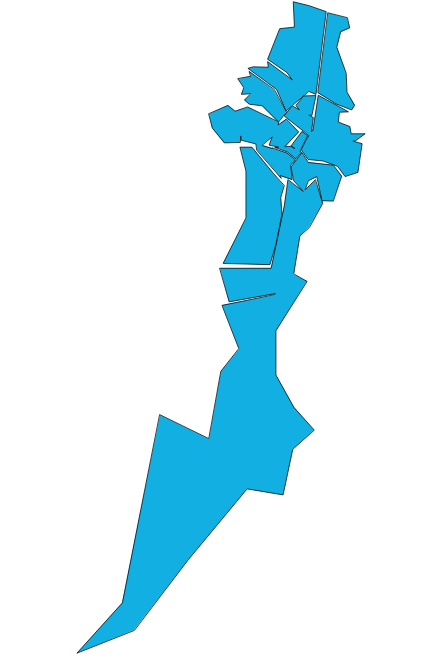
Si queremos intentar simplificar aun más esta geometría, tendríamos dos opciones:
- Utilizar GRASS para obtener una simplificación topológica de la geometría
- Utilizar la extensión topology de PostGIS. Aunque ésta es una geometría dificil de unir. No todos los polígonos están unidos y algunos se montan sobre otros, de manera que habría que jugar con el concepto de tolerancia.
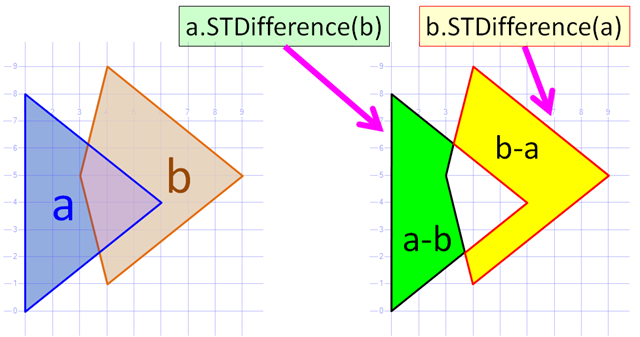
Diferencia¶
La diferencía entre dos geometrías A y B, son los puntos que pertenecen a A, pero no pertenecen a B
ST_Difference(Geometría A, Geometría B)
Diferencia simétrica¶
Es el conjunto de puntos que pertenecen a A o a B pero no a ambas.
ST_SymDifference(Geometría A, Geometría B)
Tipos de geometrías devueltas¶
El tipo de geometrías que devuelven estas operaciones no tienen porque ser igual al tipo de geometrías que le son pasadas como argumentos. Estas operaciones devolverán:
- Una única geometría
- Una geometría Multi si está compuesta por varias geometrías del mismo tipo
- Una GeometryCollection si está formada por geometrías de distinto tipo.
En este último caso habrá que proceder a una homogeneización de las geometrías que son devueltas, para ello podremos utilizar diferentes estrategias:
- El uso de clausulas de filtrado, por ejemplo indicando que solo se devuelvan aquellas geometrías cuya intersección sea una línea.
- Crear las tablas de salida de tipo Multi, en este caso las geometrías que no sean multi podrán ser convertidas a este tipo mediante la función ST_Multi
- En caso de que las geometrías devueltas sean tipo GeometryCollection, será necesario iterar esta colección, y extraer mediante la función ST_CollectionExtract las geometrías en las que estamos interesados, indicandole para ello a la función la dimensión de las geometrías.
Transformación y edición de coordenadas¶
Mediante el uso de diferentes funciones seremos capaces de manejar transformaciones entre sistemas de coordenadas o hacer reproyeciones de las capas. Para un manejo básico de estas utilizaremos las funciones que PostGIS pone a nuestra disposición:
- ST_Transform(geometría, srid), que nos permite la transformación de la geometría al SRID que le pasamos por parámetro.
- **ST_SRID(geometria) nos muestra el SRID de la geometría
- ST_SetSRID(geometria, srid) asigna el SRID a la geometría pero sin relizar la transformación
En la tabla spatial_ref_sys encontraremos la definición de los sistemas de coordenadas de los que disponemos. Podremos consultar la descripción de ellos mediante consultas select del estilo:
# select * from spatial_ref_sys where srid=4326;
Para transformar las geometrías en otros sistemas de coordenadas, lo primero que debemos saber es el sistema de coordenadas de origen y el de destino. Hemos de consultar que estos se encuentran en la tabla spatial_ref_sys. En caso de que alguna de nuestras tablas no tenga asignado un SRID, el valor de este será -1, valor por defecto, por lo que habrá que asignarle el sistema de coordenadas antes de la transformación.
Práctica¶
¿Cuál es el área total de páramos contenidos en todos los barrios de Bogotá?
¿Cuál es la longitud del rio más largo que pasa por el barrio de Suba?
Muestra el nombre de cada barrio junto con la longitud total de ríos que contiene, ordenado por longitud en orden descendiente
¿Cual es la provincia que más longitud de rios contiene?
¿Cuál es el área de páramos que contiene solo el barrio de San Cristóbal?